Acoustics Information
Intro | Sound and Decibles | | Wind Turbine Sound | Noise Impact and Regulation
Outdoor Sound Propagation
Sound travels through air at a speed of approximately 1128 feet per second or 769 miles per hour. Thus it takes just over two seconds for a sound wave to travel a half mile. The number of sound waves that travel past a given point in one second is determined by its frequency or pitch. The sound pressure level decreases or attenuates as sound spreads out and travels over distance through the air. Attenuation results from distance, atmospheric absorption, and terrain effects. The rate of attenuation due to distance or spreading of the sound wave (i.e. divergence) is the same for all frequencies, which is approximately 6 dB per doubling of distance from a simple point source.
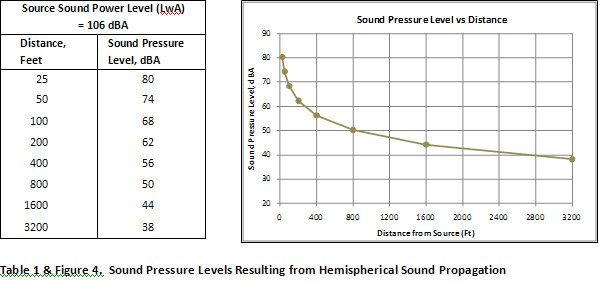
For an elevated point source, sound will radiate into a full sphere; a condition known as the free field. Once the sound reaches the ground it will spread in a hemispherical pattern resulting in a sound level that is 3 dB higher at a given distance when compared to spherical spreading. Table 1 provides the sound pressure level at various distances for hemispherical propagation of sound from a point source having a sound power level of 106 dBA. This relationship is shown graphically in Figure 4. The sound level reduction in Table 1 and Figure 4 is due only to distance and does not include attenuation from atmospheric absorption and foliage or reflection from hard surfaces.
Sound energy is absorbed by the atmosphere as it travels through the air. The amount of absorption varies by the frequency of the sound and the temperature and humidity of the air. More sound is absorbed at higher frequencies than at lower frequencies due to the relative wavelengths.
In addition to temperature and humidity, wind speed and direction can affect outdoor sound propagation. When sound travels upwind the sound waves can bend upward creating a “shadow” zone near the ground where sound levels decrease when compared to downwind sound propagation. Wind gradients, temperature inversions and cloud cover can cause refraction or bending of sound waves toward the ground resulting in less sound attenuation from terrain and ground cover over large distances.
Sound attenuation can also result from intervening terrain and certain types of ground cover and vegetation. An example of intervening terrain is a hill or ridge that blocks the horizontal sound path between a sound source and receiver. This same effect can result from buildings and other solid structures such as a sound barrier fence. Sound will also attenuate as it travels over soft ground cover or through vegetation such as trees and shrubs. The amount of ground and foliage attenuation depends on the characteristics of the ground cover and the height and density of vegetation. Conversely, reflective ground or the surface of a water body can cause reflection of sound and less overall attenuation.
When multiple sound sources are present in an area, the sound level contribution from each source must be added to determine of the combined sound level of all sources. Due to logarithmic basis of the dB unit, adding sound levels is different than standard arithmetic. Adding two equal sound sources that each measure 50 dBA at a specific point will result in a combined sound level of 53 dBA. It will then take two more equal sound sources of 50 dBA each, or four total, to cause the sound level to increase by another 3 dBA. Thus, four equal sources at 50 dBA results in a total sound level of 56 dBA.
Specifications for calculating outdoor sound propagation have been developed by international standards organizations as well as individual countries based on empirical data developed over many years. These specifications form the basis for computerized sound level prediction models that allow calculation of outdoor sound propagation through the use of three-dimensional terrain models. The most widely used and accepted standard for calculating outdoor sound propagation is ISO 9613-2 Acoustics - Attenuation of Sound During Propagation Outdoors - Part 2: General Method of Calculation. This standard has been applied to accurately calculate the sound levels that result from operation of industrial noise sources such as wind turbines.
|

